Arithmetic for Computer¶
约 3250 个字 25 张图片 预计阅读时间 11 分钟
Introduction¶
计算机中的指令可以分为三类:
memory-reference instructions
lw, sw
需要 ALU 计算内存地址
lw指的是 load word, 从内存中读取一个字,sw指的是 store word, 将一个字存入内存。
arithmetic-logical instructions
add, sub, and, or, xor, slt
需要 ALU 进行计算
slt指的是 set less than, 如果第一个操作数小于第二个操作数,那么将结果设置为 1,否则为 0。
control flow instructions
beq, bne, jal
需要 ALU 进行条件判断
beq指的是 branch equal, 如果两个操作数相等,那么跳转到指定地址。bne指的是 branch not equal, 如果两个操作数不相等,那么跳转到指定地址。jal指的是 jump and link, 跳转到指定地址并将下一条指令的地址存入寄存器。
Signed Number Formats(有符号数的表示)¶
- Sign and magnitude
- 2's Complement
- 1's Complement
- Biased notation
what is biased notation
偏置表示法(或 偏移表示法 )是一种在计算机科学中常用的数值编码系统,主要用于表示正数和负数。它通过引入一个 偏置 或 偏移量 到实际数值,使得所有编码的数字都是非负数,这样可以简化硬件实现。在浮点数表示等系统中,这种方法特别有用。
- 偏置或偏移量: 在编码时给实际数值加上一个固定的偏置。
-
编码过程:
当一个数字要被编码时,需要将其值加上一个固定的偏置。例如,如果偏置是 127,而数字是 -5,那么编码后的值将是 \(-5 + 127 = 122\)。 -
解码过程:
当需要解码时,解码器将从编码后的数字中减去偏置,以恢复原始的值。例如,编码值 122 经过解码时,减去 127 得到原始值 \(-5\)。
假设我们使用 8 位二进制数来表示数字,偏置设定为 127:
-
编码时:
- 数字 0 编码为 \(0 + 127 = 127\),即二进制表示为
01111111 - 数字 5 编码为 \(5 + 127 = 132\),即二进制表示为
10000100 - 数字 -3 编码为 \(-3 + 127 = 124\),即二进制表示为
01111100
- 数字 0 编码为 \(0 + 127 = 127\),即二进制表示为
-
解码时:
- 如果读取到
01111111,对应的值为 \(127 - 127 = 0\) - 如果读取到
10000100,对应的值为 \(132 - 127 = 5\) - 如果读取到
01111100,对应的值为 \(124 - 127 = -3\)
- 如果读取到
-
应用场景:
偏置表示法常用于 浮点数表示,尤其是在IEEE 754 标准中,浮点数的指数部分使用了偏置表示法。这使得指数可以同时表示正数和负数,简化了硬件电路的设计与实现。
偏置表示法通过添加一个固定的偏移量,使数值表示更加方便,特别是在底层硬件实现上有较大优势。
Why we need biased notation

上图是 32 位的二进制补码表示,我们可以看到左侧二进制表示,如果看作无符号数,那他们是从小到大排列的;但右侧对应的十进制整数确实分段单增的。
我们希望有一种这样的表示,能够让右侧的对应的值也单调递增。
一个想法是对右侧数加上 \(2^{31}\), 相当于其二进制表示下最高位翻转。
计算偏移码
在没有说明的情况下,\([X]_b = 2^n + X\) 从二进制码到移码,只需要翻转符号位即可。
在 IEEE 标准中,偏移码要加上 \(2^{n-1}-1\) 而不是 \(2^{n}\)
Arithmetic¶
- Addition
- Substraction(通过加法实现,减去一个数等于加上这个数的补码)
- Overflow detection:
Overflow detection
无符号数的溢出:

有符号数的溢出:

在二进制加减法中,溢出(Overflow)是指计算结果超出了可表示的数值范围,通常发生在 有符号数 运算中。
在设计加减法器时,通常在数据位的基础上再增加一位用于判断是否溢出或者进位。这一位通常称为 溢出位(Overflow Bit)或 进位位(Carry Bit)。
有符号数的溢出有以下几种情况
| Operation | Operand A | Operand B | Result overflow |
|---|---|---|---|
| A + B | ≥ 0 | ≥ 0 | < 0 (01) |
| A + B | < 0 | < 0 | ≥ 0 (10) |
| A - B | ≥ 0 | < 0 | < 0 (01) |
| A - B | < 0 | ≥ 0 | ≥ 0 (10) |
可以发现,溢出时\(C_n \oplus C_{n-1}\)即进位位和最高位的异或结果为1。
而对于无符号数,只有一种情况会发生溢出,即结果大于可表示的最大值,carry bit为1。
Key-point
当ALU使用的是加减法操作时,才有\(C_n \oplus C_{n-1}\)
Constructing an ALU
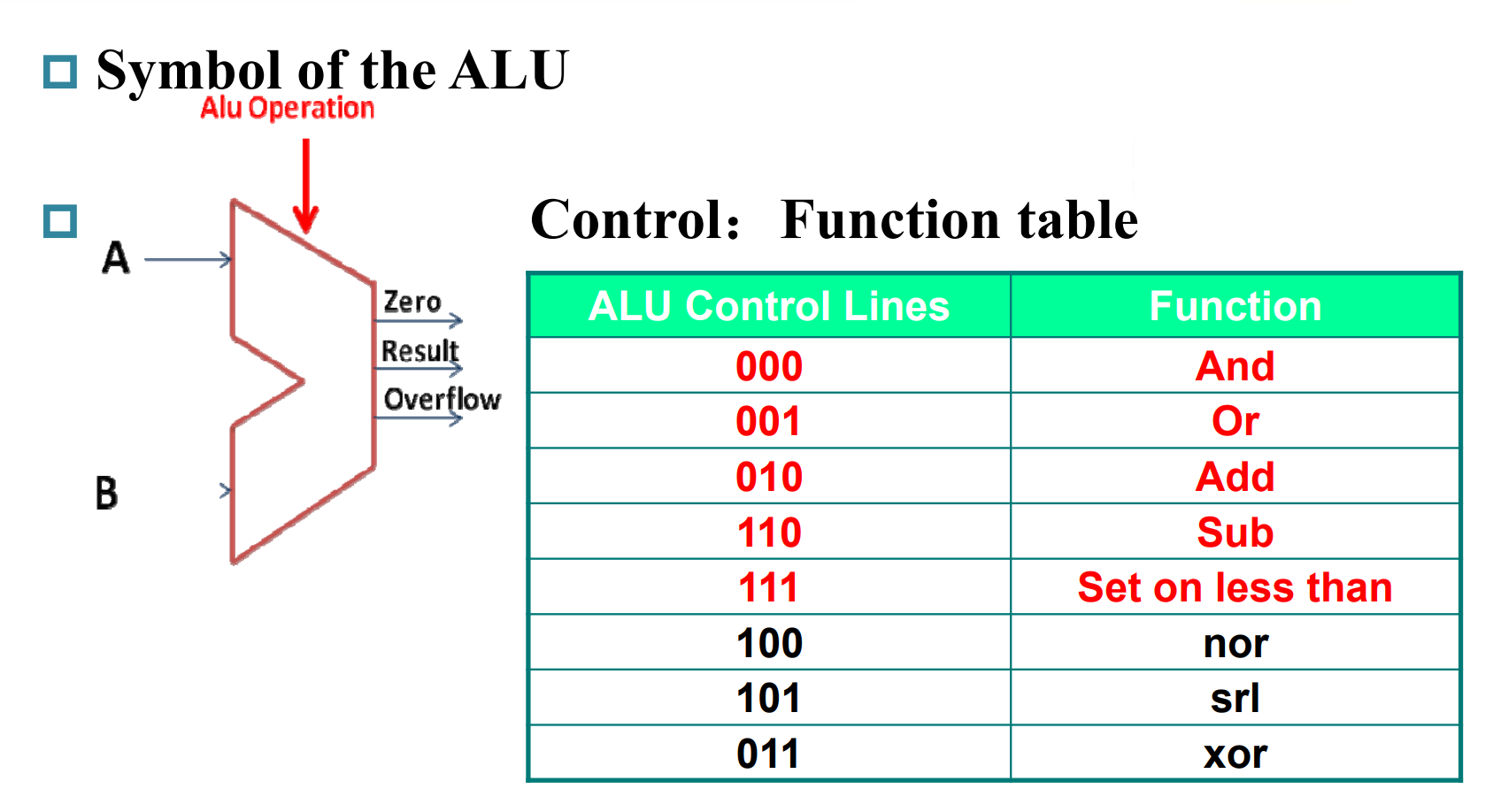
注: RISC-V 不支持 nor 指令。
Multiplication¶
Unsigned multiplication¶
Version 1
第一种乘法器,判断乘数的最低位是否为 1,如果是则被乘数加部分和存到结果里面,否则加0。每次左移被乘数,右移乘数。


需要 64+64+32 bit 的寄存器,和一个 64 bit ALU.
Version 2
在Version1中,实际上每次进行的加法都是32位的,每次加完以后,product的最低位就不会变化,因此我们可以使用32位的ALU,每次右移product而不是左移乘数,然后让乘数与product相加即可。 这样原本需要64+64+32 bit 的寄存器,和一个 64 bit ALU. 变成了 32+64+32 bit 的寄存器,和一个 32 bit ALU.

Version3
Version2中,64位的product每次右移,其中只有高32位有用,那么低32位恰好可以用来存放乘数。这样我们就可以只用32位的寄存器和ALU来实现乘法。


例-4位乘法,高四位结果,低四位乘数

Signed multiplication¶
有符号相乘不能直接乘,可以先用符号位决定结果符号,再对绝对值进行乘法。
Booth's Algorithm

思想:如果有一串 1, 减掉乘数的第一个 1, 后面的 1 的序列进行移位,当上一步是最后一个 1 时加。
最开始把积放在高位,被乘数放在低位。(数据保存方法同 2.1.1)默认 \(bit_{-1}=0\)
-
Action
- 10 - subtract multiplicand from left
- 11 - nop
- 01 - add multiplicand to left half
- 00 - nop
每个操作结束后都要移位,和 2.1.1 中类似
Key-point
需要注意的是 Booth算法中,每一次是两位两位看,对于\(n\)位的,需要进行\(n\)次操作,但是两位两位看只能看到\(n-1\)位,因此开始之前是需要在最后一位加上一个 0 再开始做乘法的
注意移位时不要改变符号位。
Example
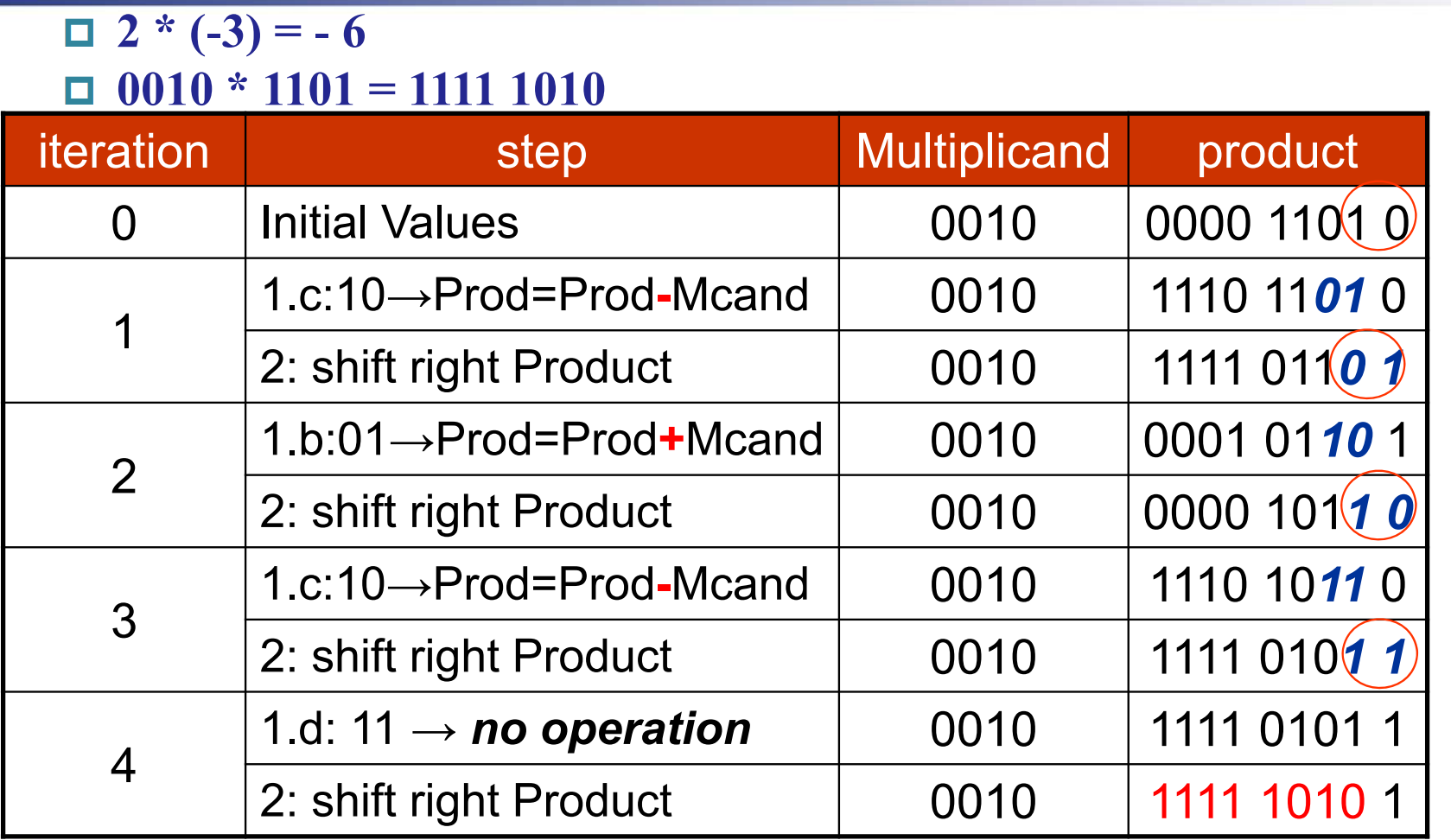
被乘数 Multiplicand 是 0010, 乘数 Multiplier 是 1101.
最开始将积 0000 放在高四位, 1101 作为乘数放在低四位。
最开始 10, 即执行减操作, \(0000-0010=1110\). 答案依然放在高四位,随后右移,以此类推。
注意右移的时候是 算术右移 ,即符号位不变。
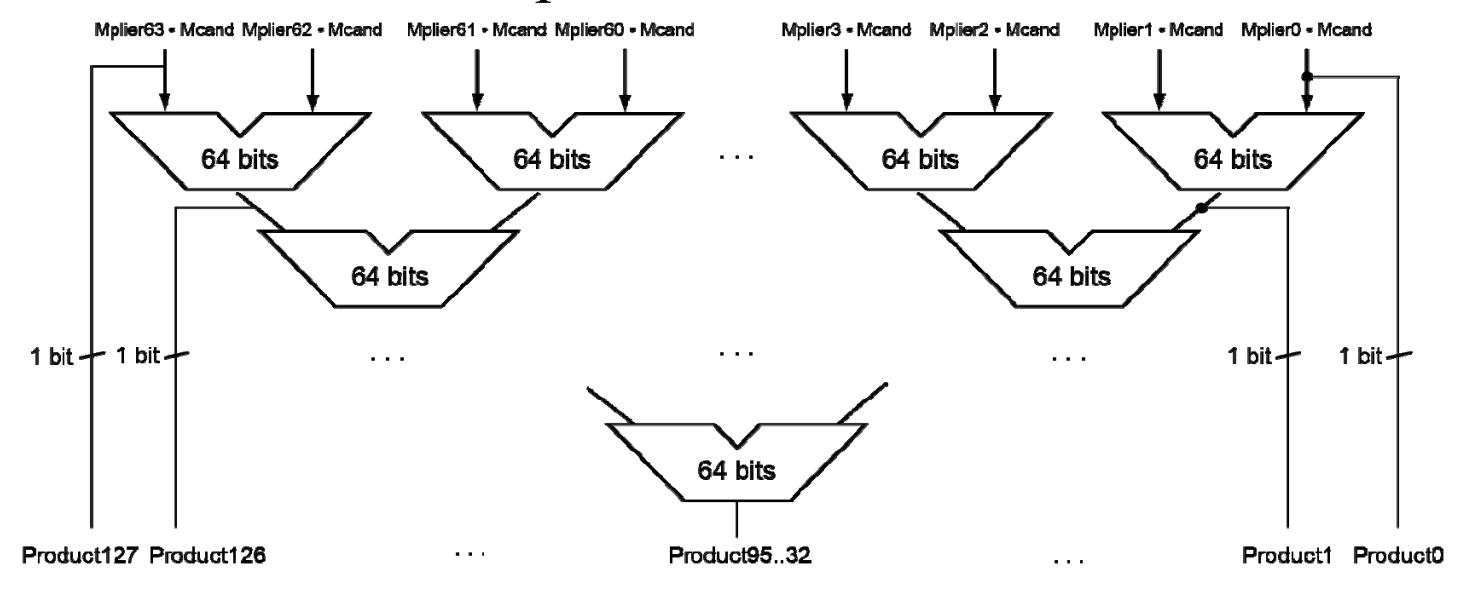
Faster Multiplication¶
32 位数乘 32 位数,相当于 32 个 32 位数相加。(并行加速)
Division¶
Version
- At At first the divisor is in the left half of the divisor register,the dividend is in the right half of the remainder register.
- Shift the divisor right each step

即对每一步,都在余数中减去除数,如果结果大于等于0,那么商左移上1,否则将结果加回去,商左移上0。
需要注意的是,由于一开始remainder寄存器右边是被除数,divisor寄存器左半边是除数,前很多次的结果都是负的
7 / 2
\(00000111 / 0010\)

Version
优化过程与乘法类似,因为每次都是remainder的最高位在减,减完就没用了,可以移出去,不再右移divisor,而是左移remainder,并且将quotient也存在Remainder寄存器每次左移产生的空位中


Key-point
remainder 寄存器其实要多一位的,因为最后一步要右移,不能直接把它丢掉
Eg

!!!question "为什么除法的移位这么奇怪“ 对于Version1,要进行 \(n+1\) 次的移位,是为了在最后一步将商补全,同时也抵消最后一步的影响来满足余数的正确性; 对于Version2,要进行第一次的整体左移是为了得到正确的余数,而在最后一步中,由于商还要进来,余数会多出一位,因此要左半部分右移一位。
对于有符号数的除法,用绝对值来做,然后在结果上加上符号位
sign of quotient = sign of dividend \(\oplus\) sign of divisor
sign of remainder = sign of dividend
Floating point number¶
进制转换
二进制小数转十进制,如果是科学计数法,可以先仿照十进制的科学计数法用指数进行小数点的移动,然后再转换,这样可以减少计算小数的次数。
十进制转换二进制,可以先转换整数部分,再转换小数部分,小数部分可以依次与\(2^{-n}\)比较,如果大于等于,那么结果的第 n 位为 1,否则为 0,上了 1 之后,要减去 \(2^{-n}\),再继续比较,直到达到精度的要求。
| S | exp | frac | |
|---|---|---|---|
| Float(位数) | 1 | 8 | 23 |
| Double(位数) | 1 | 11 | 52 |
Normalized form: \(N=(-1)^S\times M\times 2^E\)
- S: sign. \(S=1\) indicates the number is negative.
- M: 尾数. Normally, \(M=1.frac=1+frac\).
- E: 阶码. Normally, \(E=exp-Bias\) where \(Bias=127\) for floating point numbers. \(Bias = 1023\) for double.
Key-point
- 为什么要把 exponent 放在前面?(因为数的大小主要由 exponent 决定。)
- 为什么需要 Bias?(移码)可以不保存负数,用的是IEEE标准,即对于8位的移码,\(Bias=2^{7}-1=127\),对于11位的移码,\(Bias=2^{10}-1=1023\)。
- 以上是规格化数,尾数前应该有前导 1,就类似于十进制的科学计数法,前导必须大于0小于10.对于2进制,前导必须大于0小于2,也就是1.
Denormal Numbers¶
- \(Exponent=000\ldots 0\)
非规格化数,让数在较小时能逐渐下溢出,在Exponent的部分以全零作为保留字,但是并不代表指数是0,而是说此时的小数不是1.xxxx而是0.xxxx。
\(x=(-1)^s\times((0+Fraction)\times 2^{1-Bias})\)
注意此时指数是 \(1-Bias=-126/-1022\).

Precision¶
- signle: approx \(2^{-23}\)
\(23\times \log_{10}{2} \approx 23\times 0.3 \approx 7\) demical digits of precision. - double: approx \(2^{-52}\)
\(52\times \log_{10}{2}\approx 52\times 0.3 \approx 16\) demical digits of preicsion.
Limitations¶
- Overflow: The number is too big to be represented
- Underflow: The number is too small to be represented
Floating-Point Addition¶
-
Alignment
统一指数,一般小的往大的变。因为系统精度位数有限,如果将大的往小的变,那可能会因此损失较大。Example

-
The proper digits have to be added
- Addition of significands
- Normalization of the result
- Rounding
Example

FP Adder Hardware
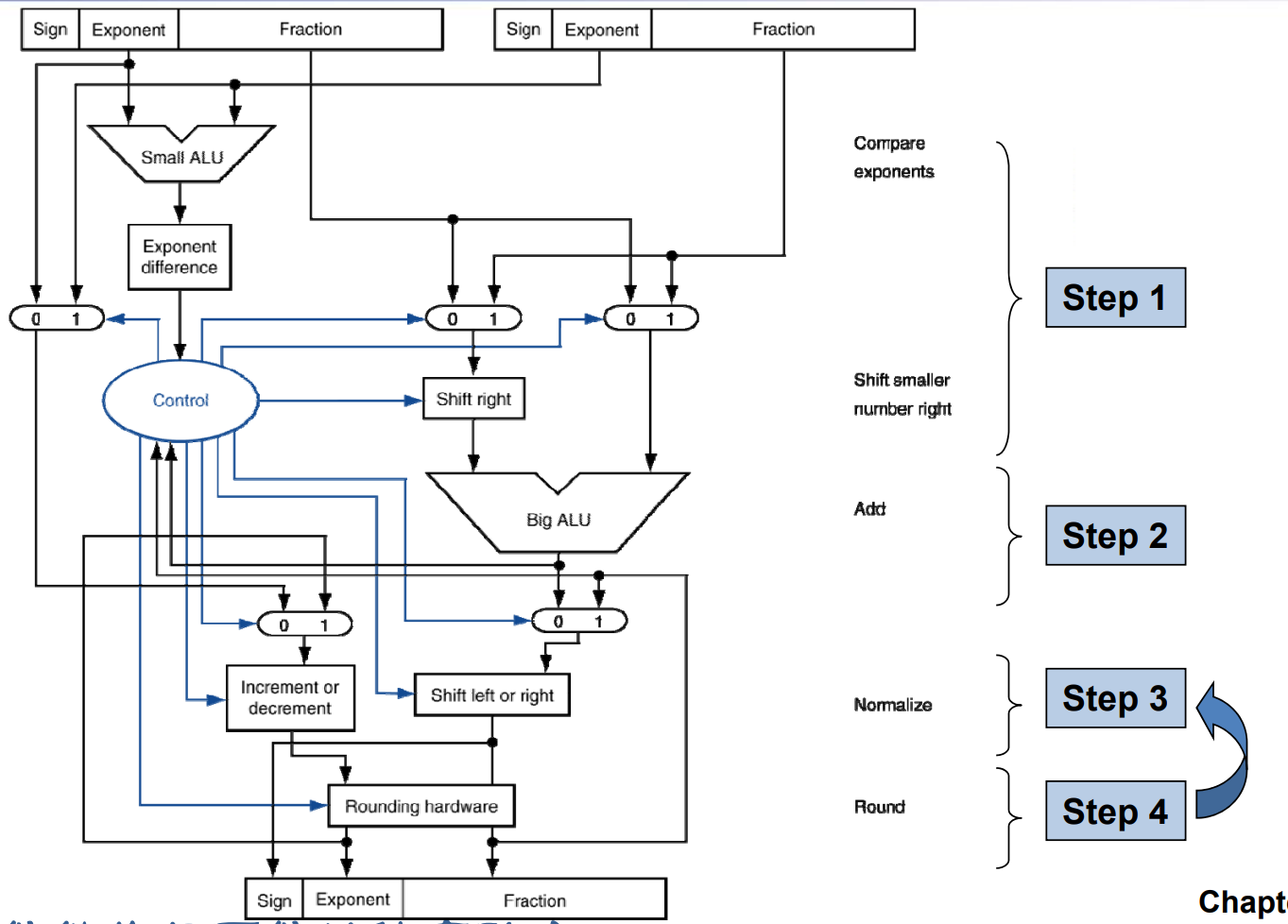
- step 1 在选择指数大的,并进行对齐。同时尾数可能还要加上前导 1.
- step 3 是对结果进行标准化。
- 蓝色线为控制通路,黑色线为数据通路。
Floating-Point Multiplication¶
\((s1\cdot 2^{e1}) \cdot (s2\cdot 2^{s2}) = (s1\cdot s2)\cdot 2^{e1+e2}\)
- Add exponents
- Multiply the significands
- Normalize
- Over/Underflow?
有的话要抛出异常,通过结果的指数判断。 - Rounding
- Sign
注意
Exponet 中是有 Bias 的,两个数的 exp 部分相加后还要再减去 Bias.
Example

Data Flow
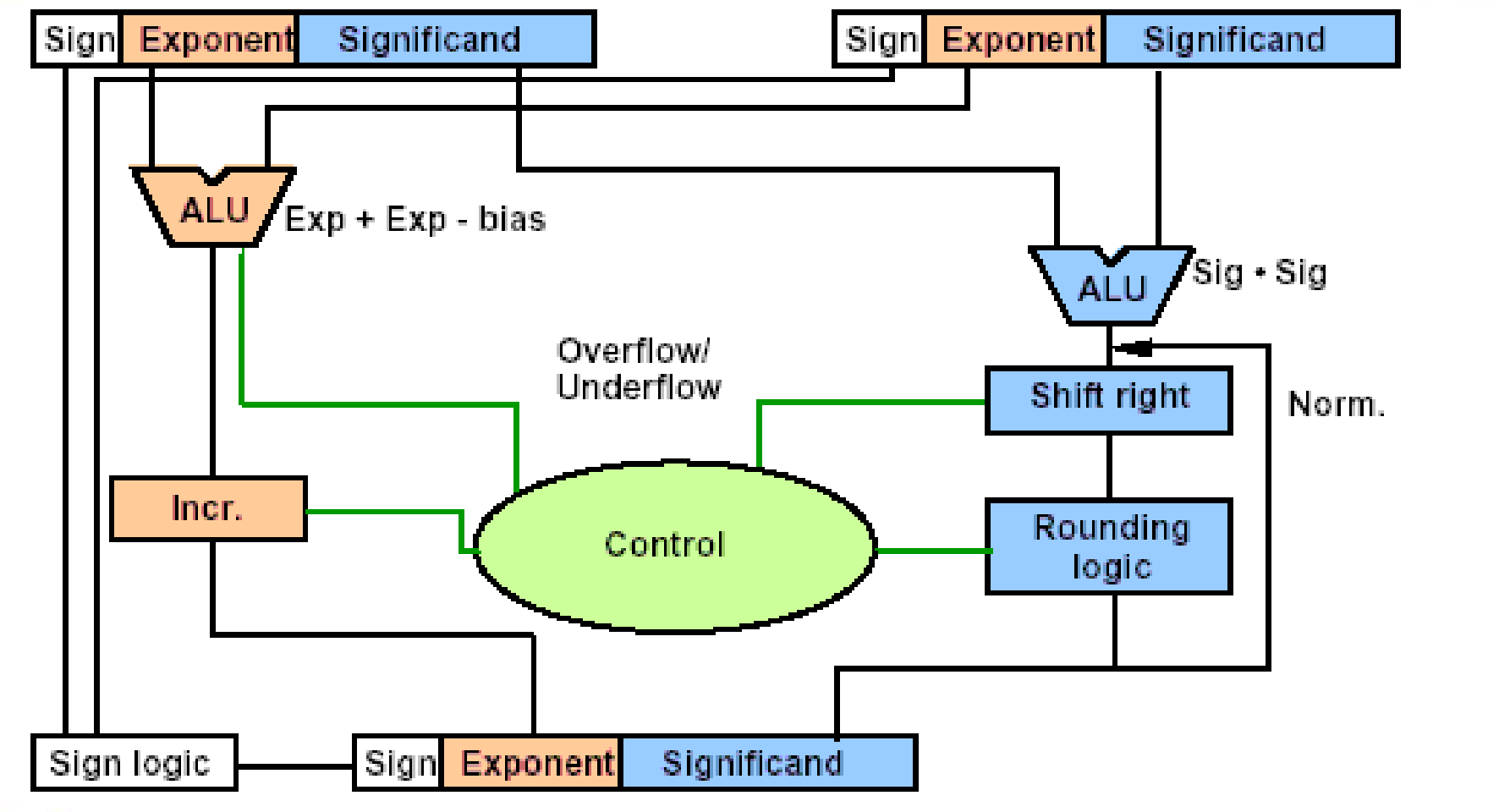
- 右边往回的箭头: Rounding 后可能会进位。
- Incr 用于标准化结果,与右侧 Shift Right 配合。
Accurate Arithmetic¶
- Extra bits of precision (guard, round, sticky)
- guard, round
为了保证四舍五入的精度。
结果没有,只在运算的过程中保留 - sticky
末尾如果不为全 0, 则 sticky 位为 1, 否则为 0.
- guard, round
Example
Guard, round, sticky 位的作用 保留位和舍入位的作用可以提高精度,例如十进制中如果加上舍入位,那么在51和99之间的会向上舍入,而在50和00之间的会向下舍入,这样可以减少误差。 例如2.34+0.0256=2.3656,舍入为2.37,而2.34+0.02=2.36,舍入为2.36,存在1ulp的误差; 在有些情况下,结果左移之后将保护位变成了最低位,只剩下舍入位一位来进行舍入,这样会导致误差增大,而加上sticky位,可以保证在舍入位后面的位数不为0时,舍入位不会被舍去,从而提高精度。例如如果是2.34+0.0050001,如果没有sticky位,那么结果是2.3450,舍入到最近的偶数2.34,而有了sticky位,知道结果是比2.3450大,舍入到最近的偶数2.35。
在二进制中,就是1进0舍,例如小数点后第三位为最低位的1.100_10+0.000_00_11111=1.100_10,此时Guard位为1,Round位为0,Sticky位为1,如果没有sticky位,那么结果就是舍入到最近的偶数1.100,而有了sticky位,知道结果是比1.100_10大,舍入到1.101。
Key-point
总的来说,G位如果等于进制的一半,则看它的下一位R位,如果R位大于0了,那么进位,如果为0,那么看S位,如果S位大于0,那么进位。如果RS位都是0了,那么选择最近的偶数来进位。(LSB是奇数,进位;LSB是偶数,舍去屁股后面的)
损失不会超过 0.5 个 ulp.